Editorial
Crypto Currency Derivatives
EUR-USD options traders are complaining about very low volatilities around 7.5% and find it hard to interpret given the political circumstances. But for all of those who prefer higher volatilities, there is an instant solution: crypto currency options have started trading a while ago with volatilities by a factor 10 higher, e.g. 75% for bitcoin, as shown in Figure 3.
Those of us who got very rich or very poor with bitcoin trades in a short period of timewill remember the spot exploding at the end of 2017 and declining sharply thereafter, see Figure 1.
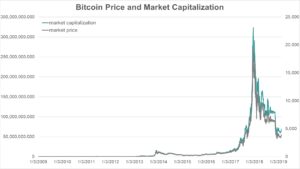
Figure 1: Bitcoin price and market capitalization, sourced from blockchain.com
Therefore, one of the puzzling questions is whether crypto currencies will remain or are going to fade away. I have been requested by many of our conference participate to cover crypto currencies before they cease to exist. The argument that a traditional currency, called a fiat currency (from Latin “let there be money”), is safer because it is backed by the central bank is not very convincing to me, as our today’s currencies are merely based on many users believing in its value, whereas actually there is no intrinsic value. At the end it is the community of users setting up its own trust system. Similarly, this would apply to crypto currencies. I don’t see why a fiat is the overall better technology.
One of the advantages is that crypto currencies can’t be multiplied arbitrarily (whereas central bank money can). Figure 2 shows the volume of bitcoin in circulation since 2009 clearly indicating a limit being approached, in spite of the bitcoin run end of 2017.
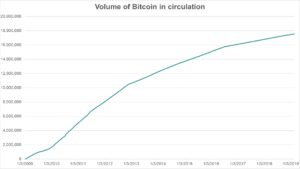
Figure 2: Volume of Bitcoin in circulation since 2009, sourced from blockchain.com
The increased interest in crypto currencies has surely called for derivatives such as tracking certificates, short crypto payoffs (at the end of 2017) and more generally options to leverage investments even more. We spot that about 5000 bitcoin vanilla options trade on deribit.com within 24 hours.
We illustrate in Figure 3 how many implied volatilities are quoted on the strike space and how a simple SVI fit could look like. We notice that
- the options market appears more like in equity derivatives, with many implied volatilities quoted on the strike space for fixed maturities;
- given the overall levels of volatility, the smile effect is rather insignificant, i.e. relative risk reversals (RR/ATM) are small;
- fitting the volatility smile depends on the input strikes: it appears that for lower strikes the put-call parity is violated, but we notice again that any theoretical mismatches do not constitute a real arbitrage opportunity in practice as the bid-offer spreads are wide and liquidity is low. Furthermore, it appears there is no liquid forward market for bitcoin, but there is an active futures and options market. This can be considered yet another difference between crypto- and fiat currencies.
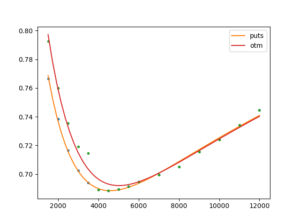
Figure 3: Fitting a volatility smile on the bitcoin strike space using either only put options or only out-of-the-money (OTM) options. Greek dots are implied volatilities sourced from deribit.com on 17 January 2019, implied volatilities for maturity 28 June 2019 (161 days) on the y-axis.
Whether and how to apply traditional volatility smile construction known and established in the currency or equity options market is yet to be clarified. Of course, one can interpolate and extrapolate volatilities using SVI, vanna-volga, non-parametric statistics, kernels, splines or any of the usual suspects. However, one must keep in mind that the Black-Scholes implied volatility originally comes from a Black-Scholes model, which rests on many assumptions including a perfectly liquid underlying market and normally distributed returns. Crypto currency prices are just very far away from such idealized assumptions. Thus, the success of translating traditional techniques to unknown terrain is yet to be tested.
On this year’s MathFinance Conference on 8-9 April we will have a symposium on crypto currencies, derivatives pricing, risk management, volatility forecasting, followed by a panel discussion with founders of a crypto currency exchange, and expect many delegates with a distinct interest in this field. I am curious myself to find out more and hope to see you in Frankfurt.
Uwe Wystup
Managing Director of MathFinance
Upcoming Events
MATHFINANCE CONFERENCE 2019
Date: April 08 – 09, 2019
Venue: Frankfurt School of Finance & Management, Adickesallee 32-34, 60322 Frankfurt am Main
MathFinance Conference has been successfully running since 2000 and has become one of the top quant events of the year. The conference is specifically designed for practitioners in the areas of trading, quantitative and derivatives research, risk and asset management, insurance, as well as academics.
As always, we expect around 100 delegates both from the academia and the industry. This ensures a unique networking opportunity which should not be missed. A blend of world renowned speakers ensure that a variety of topics and issues of immediate importance are covered.
Our confirmed speakers for 2019 include:
- Dr. Marcus Becker (Deloitte): Arbitrage and Non-linear Taxes
- Dr. Mark Beinker (d-fine): Derivative pricing: A pattern-matching problem?
- Prof. Griselda Deelstra (University of Brussels): Mutivariate FX models with jumps: Triangles, Quantos and implied correlation
- Prof. Dr. Wolfgang Härdle (Humboldt University of Berlin): Pricing Cryptocurrency Options: the Case of CRIX and Bitcoin
- Junjie Hu (Humboldt University of Berlin): Realized Cryptocurrency Volatility Forecasting with Jumps: An Empirical Study
- Prof. Dr. Karel in’t Hout (University of Antwerpen): Numerical Valuation of Bermudan Basket Options via Partial Differential Equations
- Dr. Antoine Jacquier (Imperial College London): VIX Options in Rough Volatility Models
- Vadim Kanofyev (Bloomberg): Machine Learning for Factor Investing
- Dr. Ingo Mainert (Allianz): Current Challenges and Developments of the Investment Industry
- Maximilian Mair (Unicredit): Application of Machine Learning for Market Making
- Dr. Jacopo Mancin (Barclays Capital): Volatility Swaps: PDE Pricing Improvements for LSV Frameworks
- Dr. Daniel Oeltz (Rivacon): Pailab – audit, revisioning and analysis of machine learning in finance
- Dr. Alla Petukhina (Humboldt University of Berlin): Portfolio Optimization with Modified CoVar in Cryptocurrency Market
- Prof. Rolf Poulsen (University of Copenhagen): The Fed Isn’t Federal – And Other Odd Things in Finance
- Prof. Dr. Thorsten Schmidt (University of Freiburg and MathFinance): Statistical Arbitrage
- Dr. Martin Simon (Deka Invest): Stock Price Bubbles – An Option-based Indicator
- Frank Thole (Wepex): Practical and quantitative issues to be solved trading and risk managing crypto assets
- Dr. Niels Wesselhöfft (Humboldt University of Berlin): The Growth-Optimal Portfolio for Cryptocurrencies
- Prof. Dr. Uwe Wystup (MathFinance): FX Options Greeks unlimited
Please click here for registration (single / group):
Academics pay 525 EUR (+VAT) at all times. We kindly ask for proof of your affiliation.
Group prices (3 or more from the same institution) are at EUR 735 (+VAT) pp.
Single tickets from February 22, 2019 is EUR 1.050 (+VAT).
Details of the conference can be found here.
