Arbitrage in the Perfect Volatility Surface
Constructing the FX volatility surface is an ongoing challenge in the derivatives industry, even for quants – or should I say, only for quants, because I am quite sure the vast majority of the population couldn’t care less? Starting from at-the-money volatilities (ATM), risk reversals (RR) for 25- and 10-delta, butterflies (BF) or strangles for 25- and 10-delta, we need to find a smile curve, and taking term structure into account, a volatility surface that prices these quoted market instruments correctly and satisfies a number of conditions including but not limited to:
- Smoothness, ideally up to second order: to construct a local volatility model
- Reasonable slope on the wings: to match prices of variance swaps
- Reasonably rich to reflect negative market strangle quotes
- Extendable to a consistent spreading logic
- Free of arbitrage
The smile construction interacts with the choice of interpolation and extrapolation. The following methods have reasonably sized fan-clubs:
- Cubic splines: easy to do, common technique, fits all the points
- Polynomials including the parabola on the forward delta space proposed by Malz 1997
- Vanna-volga for interpolation proposed by Castagna/Mercurio
- Kernels
- Stochastic volatility models, most prominently SABR and its numerous patchwork extensions for wings
- Stochastic volatility inspired (SVI) parametric fits proposed by Gatheral
While it will take a long time to check and vet all the methods, today, I would like to direct your attention to a few highlights, aiming to correct some common misconceptions.
1. The first figure visualizes the differences between the popular cubic spline interpolation and MathFinance’ MFVal interpolation. We observe that there is actually some concavity in market volatilities when going far OTM and plotting implied volatility on the log-moneyness space instead implied volatility on the delta space. The non-smooth shape of the implied density is a consequence of cubic spline being smooth up-to second order only (i.e. 3rd derivative may be discontinuous).
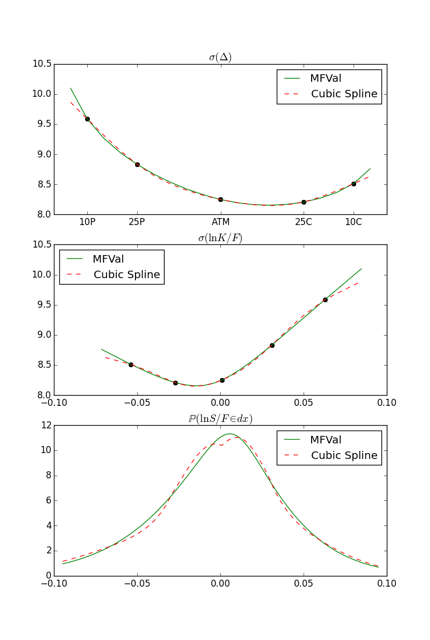
We show EUR/USD volatility interpolation of 31 October 2016 for the 3M tenor. We show: top: implied volatilities on the delta space; middle: implied volatilities on the log-moneyness space; bottom: implied probability density of the final spot price on the log-moneyness space.
In a sense the fit using cubic splines is too good: matching all the points can lead to non-unimodal densities – look at the dent in the density near the 0.00 point – , even if the fit of the smile curve passes the mere-eye-visual-inspection-sanity-check.
2. Since cubic splines might overdo the fit, another fan club in the market uses Gatheral’s SVI and their various offspring, a parametric curve inspired from stochastic volatility models. Here, we can match many desirable conditions imposed on the smile curve, and it will at the very least usually look nice.
However, it is not necessarily arbitrage-free. In fact: even a nice fit that passes the mere-eye-visual-inspection-sanity-check, with supposedly steep slopes on the wings may not be free of arbitrage. Consider the example of a Butterfly Arbitrage possibility on SVI smile for AUD/NZD 1W options on 2014-Jul-02 ¹. We see perfect fit, but as shown in the graph, the low delta put side admits Butterfly Arbitrage or equivalently, implies a negative probability density of the 1W spot, indicated in red in the lower graph lower LHS.
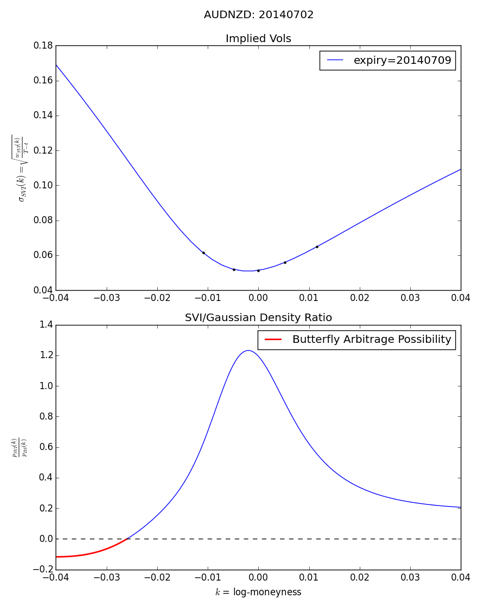
Conclusion: Visual inspection of the smile fit helps, and should be done if possible, but even that plus a perfect fit of the 5-point market do not guarantee unimodal densities or arbitrage-free smile surfaces.
On the next MathFinance Conference, part of our panel discussion will cover the survival techniques for banks and their trading desks, the volatility surface being one of the key success factors. Technology, technology, technology. Hope to see you on 20/21 April in Frankfurt.
Alexander Stromilo and Uwe Wystup, MathFinance
¹ Spot reference = 1.0784, fwd = 1.07845, AUD discount factor = 0.999712587139, 10-delta RR = 0.35%, 25-delta RR = 0.40%, ATM vol = 5.14%, 25-delta BF = 0.25%, 10-delta BF = 1.175%
Upcoming Events
Dear MathFinance Community,
we would like to update you on the current agenda of this year’s MathFinance Conference taking place on April 20-21, 2017 in Frankfurt.
Besides the attractive list of world renowned speakers we will have a Symposium on Numerical Methods arranged by Prof. Karel in’t Hout covering the following topics:
- Complexity Reduction Techniques for Finance by Prof. Dr. Kathrin Glau (Technical University of Munich)
- On an efficient one and multiple time-step Monte Carlo simulation of the SABR model by Álvaro Leitao (University of Delft)
- Calibration of a Four-Factor Hybrid Local-Stochastic Volatility Model with a New Control Variate Particle Method by Matthieu Mariapragassam (University of Oxford)
- ADI Finite Difference Schemes for the Calibration of Stochastic Local Volatility Models: An Adjoint Method by Maarten Wyns (University of Antwerp)
In addition, Uwe Wystup will discuss with Christoph Burgard and Wolfgang Gerhardt in a panel “Recent Advances in Derivatives Technology. What do we need to run a successful derivatives business in the current environment?”
Tickets will be EUR 990 (+VAT). Academics pay EUR 495 (+VAT) at all times.
Group prices (3 or more from the same institution) are at EUR 693 (+VAT) pp.
All information, including the speakers, talk abstracts, ticket prices etc. can be found on our website (www.mathfinance.com) or check out our conference brochure.
Should you have any further questions please do not hesitate to contact us, either by email to conference@mathfinance.com or by calling +49 69 6783 17200.
D-FINE DAY FRANKFURT
EINBLICK IN DIE RISIKOMANAGEMENTBERATUNGSPRAXIS
Die Dynamik der Finanzwelt ist ungebrochen: Unsicherheit an den globalen Finanzmärkten durch Treiber wie anhaltende Euro-Krise, Turbulenzen am Rohölmarkt und negative Zinsen stellt Geschäftsstrategien und Risikomodellierung vor eine schwere Prüfung. Eine Flut neuer Regularien verändert die Rahmenbedingungen, und neue Technologien verändern unser Zahlungs- und Investitionsverhalten maßgeblich. Wollen Sie verstehen, was sich dahinter verbirgt und vielleicht den Wandel mitgestalten? Dann sollten Sie d-fine näher kennenlernen. Denn mit solchen Themen und vielen weiteren spannenden und anspruchsvollen Fragestellungen beschäftigen sich unsere Berater (m / w). Und sie beantworten die an sie gestellten Fragen durch die Kombination von Methoden und Modellen aus Ökonomie, Mathematik und Physik. Wissenschaft und Unternehmen, alles ist ständig in Bewegung.
Es gibt noch viel Platz für neue Denkansätze und unkonventionelle Ideen bei d-fine. Registrieren Sie sich auf unserer Homepage bis zum 17. April 2017. Je früher desto besser, denn die Teilnehmerzahl ist begrenzt. Wenn Sie also gerade dabei sind, Ihre akademische Karriere mit einem exzellenten Abschluss (MSc, Diplom oder Promotion) zu krönen und bereit sind, einen Schritt über die Grenzen zwischen Naturwissenschaft und Unternehmenspraxis zu gehen, dann sind wir gespannt auf Sie.
d-fine ist ein führendes europäisches Beratungsunternehmen mit Standorten in Frankfurt, München, London, Zürich und Wien. Mit über 600 hochqualifizierten Beratern unterstützen wir unsere Kunden – Banken, Versicherungen und Industrieunternehmen – bei anspruchsvollen quantitativen, prozessualen und technologischen Herausforderungen. Strategieberatung, Fachberatung, Technologieberatung: d-fine ist alles in einem.
d-fine. Die Spezialisten für Risk&Finance
½-tägiger Workshop mit finanzmathematischen Vorträgen zum Themenkomplex Kontrahentenrisiko und Erfahrungsberichten aus unserer Consulting-Praxis. Bewerbungsschluss ist der 17. April 2017.
Montag, 24. April 2017
Adina Apartment Hotel Frankfurt
Neue Oper
Wilhelm-Leuschner-Straße 6
60329 Frankfurt am Main
d-fine GmbH
Svenja Dröll
An der Hauptwache 7
60313 Frankfurt am Main
T +49 69 907 37-555
www.d-fine.de
Frankfurt, München, London, Zürich, Wien
Careers
MathFinance Openings
Senior Quant/ Consultant
We are looking for senior quant/ consultant in the areas of
Insurance
- Actuary with 5 to 7 years of experience in insurance or re-insurance
- Experience in quantitative Risk Management in relation to regulatory issues (Solvency II)
- Experience in Capital Management
Banking
- Quant with 5 to 7 years of experience in Banking, ideally in Trading
- Experience in quantitative Risk Management in relation to regulatory issues (Basel III)
- Experience in Capital Management
Investment
- Quant with 5 to 7 years of experience in Asset Management (Funds, Insurance and Family Offices), ideally with emphasis on Risk Management
- Experience in quantitative Risk Management in relation to regulatory issues (German KAGB and KARBV)
Please send us your CV to recruitments@mathfinance.com
Junior Quant
Do the following apply to you?
- Master degree or diploma in (business) mathematics or physics
- PhD or CFA is a bonus
- First experiences in mathematical finance is desirable
- Very good programming skills, e.g. C++, Python or Matlab
- Good language skills in German and English
- Outstanding analytical skills and a problem-solving attitude
- High motivation to develop your knowledge and skills
- Good communication skills and team spirit
Then we would like to hear from you. Please send us your CV to recruitments@mathfinance.com
