How can a 50/50 bet have a profit of 70%?
A digital call (put) option with a strike at-the-money (ATM) pays 1 USD if the price of the underlying is at or above (below) the strike at maturity. Ignoring a drift (caused by the forward curve), one would expect a profit to be 100%. Digitals trade on many underlyings including FX, commodities, equities, precious metals, stock indices, even a geometric Brownian motion. Nowadays they are even available to retail investors on bank platforms or even non-bank vendors.
The following questions were put forward to me by Rolf Poulsen:
- Q1: What is the initial price of the digital option given the potential profit is 70%?
- Q2: Is that price consistent with the Black/Scholes (or small-step-standard-binomial) model?
- Q3: Which simple model can explain a 70% potential profit?
- A1: A pay-off 1unit of domestic currency is the only case with a positive rate of return, so the price p must solve (1-p)/p = 70%, i.e. p = 0.588. Interestingly this is not 0.500, which is what one might expect for a 50/50-type of a bet. And a bid-offer spread alone does not explain this difference.
- A2: In such models the price of an ATM digital option goes to 0.5 as time to expiry goes to 0. So, the answer is no, unless we admit fairly unrealistic scenarios for interest rate and volatility.
- A3: So how do we explain this? A price (in the sense of MTM) of 60% for an ATM spot digital (paying DOM, domestic currency) is easily possible. When you calculate the Black-Scholes value with the ATM volatility you would get 50%, but the smile leads to the windmill effect for digitals. The windmill adjustment is – VanillaVega multiplied by the slope of the smile on the strike space. Since VanillaVega is always positive and peaks ATM, the sign of the adjustment is opposite to the slope of the volatility smile (viewed on the strike space), so for a negative risk reversal, the windmill will blow the price up. In the example, the market expectation is that oil prices will go down, which is typically reflected by a negative risk reversal. Wind blows about 5%-10% upwards; hence a 58.8% price is perfectly market consistent. I am using rates close to zero for oil and USD, so forward = spot, and ATM volatility of 10% for the sake of example. This is nothing really extreme.
How does it work as time to maturity goes to zero? Can we still have deviations of the same size?
Let’s consider a popular educational model for smile interpolation: the parabola suggested by A. Malz, which is a function of volatility on the forward delta call space, known as σ(Δ)=ATM-2RR(Δ-50%)+16BF(Δ-50%)², where Δ denotes the forward call delta, RR the 25-delta risk reversal, BF the 25-delta butterfly. Here is your job for the weekend: assuming ATM, RR, BF stays the same as time to maturity goes to zero, verify that under this parabolic smile model, the limiting windmill adjustment is –RR/(πATM) for the delta-neutral ATM strike.
If RR is -1.5% and ATM 10%, then this windmill adjustment is roughly 5%, which would bring the price up from a theoretical value of 50% to a market value of 55%. A higher risk reversal could cause an even higher up-wind. With a bid-offer spread included, a price of 58% can easily be explained.
This might be quite hard to explain with more sophisticated models based on jump-diffusion or stochastic volatility.
Note, that for very short maturities, this is only a very theoretical result, because for O/N options vega is essentially not tradable, and the smile surface will very likely look different from the 1M or 1W tenor.
For example, EUR-USD data of 30 March 2017 for the tenors, O/N (red), 1W (pink), 1M (olive) with a cubic spline interpolation indicates how different market data can look like for the very short term. We show implied volatility on the delta-space (and obviously do not want to argue that cubic splines are necessarily the best choice of interpolating).
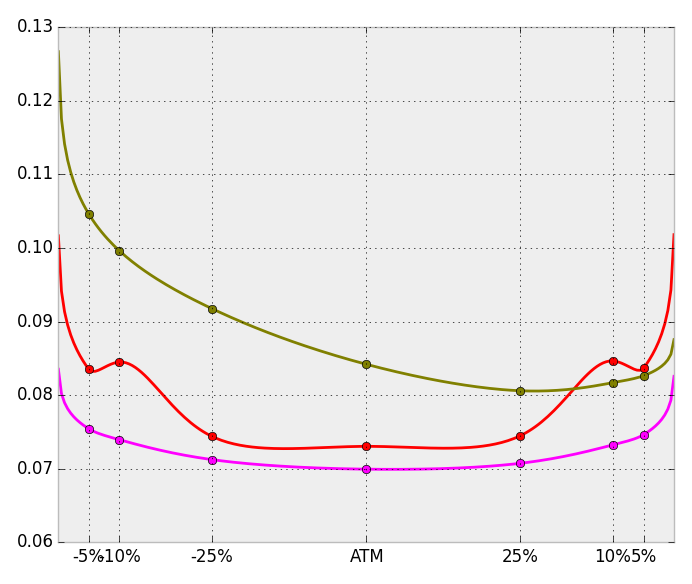
The volatility surface is the key object for option pricing, not only vanilla options, but also exotic options, such as a simple digital.
Our next flow event on 29 June 2017 will be an FX Volatility surface 101 exam. We will discuss FX volatility market data and how to analyze and handle it. If you are interested in participating, please contact our Frankfurt office at info@mathfinance.com.
Uwe Wystup, Managing Director of MathFinance
Upcoming Events
MATHFINANCE FLOW EVENT
Mainluststraße 4 – 60329 Frankfurt am Main
Date/Time: 29 June 2017 – 18:00
Title: FX Volatility 101 Exam
Presenters: Alexander Stromilo, Andreas Weber and Uwe Wystup
FX volatility market data originates from OTC transactions/quotations from major market makers, typically quoted as at-the-money volatilities, risk reversals and butterflies in some currency pair dependent conventions. Data providers collect these data, convert or treat them in a proprietary way, potentially average them and often make results available in their own standardized currency-pair independent conventions.
In this flow we would like to increase awareness of the issues arising from the fact that market data varies in quality and format depending on the provider and averaging methods. Data providers we consider include Reuters, DigitalVega, Tulletts, and SuperDerivatives, and they all have their own characteristics. Subsequently, if a quant’s job is to build a smooth and ideally arbitrage-free volatility surface, we show how FX smile conventions need to be treated, how different interpolation techniques handle the input data. We will present some graphs that allow visual detection of butterfly- and calendar-arbitrage.
Some topics for discussion include short dated volatilities:
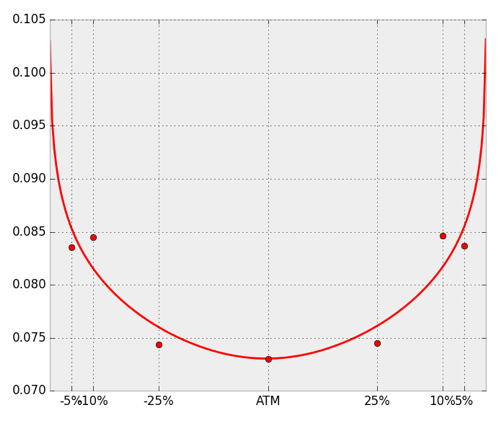
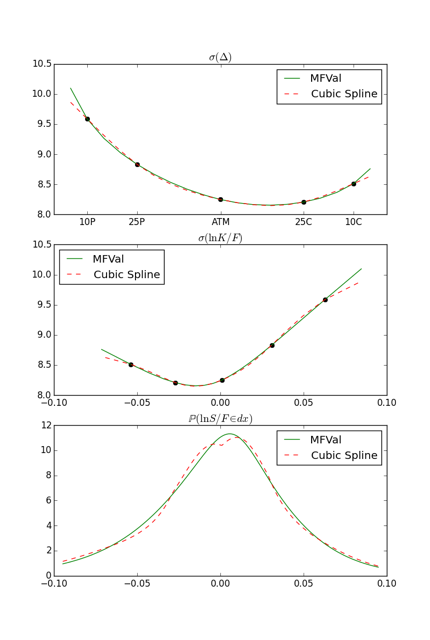
cubic spline based interpolations can cause oscillations and potentially non unimodal probability densities: spline vs. parameterized curve.
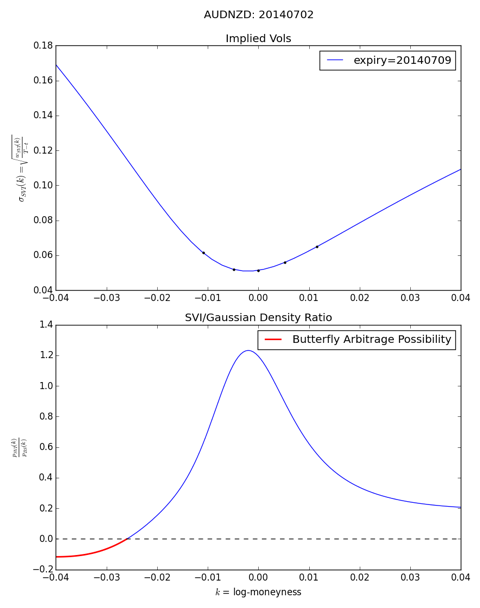
SVI traps: potentially, SVI may imply a negative probability density even if the curve looks perfect by visual inspection.
If you are interested in attending please send an email to info@mathfinance.com.
The event is by invitation only, but we have a small number of seats free for interested participants. The event is free of charge, but we do ask you to reserve a spot by emailing us. As a courtesy to other interested participants, kindly inform us ahead of time should you be unable to attend.
D-FINE DAY HAMBURG
EINBLICK IN DIE RISIKOMANAGEMENTBERATUNGSPRAXIS
Die Dynamik der Finanzwelt ist ungebrochen: Unsicherheit an den globalen Finanzmärkten durch Treiber die anhaltende Euro-Krise, Turbulenzen an Energie- und Rohstoffmärkten und negative Zinsen stellt Geschäftsstrategien und Risikomodellierung vor eine schwere Prüfung. Eine Flut neuer Regularien verändert die Rahmenbedingungen, und neue Technologien verändern unser Zahlungs- und Investitionsverhalten maßgeblich. Wollen Sie verstehen, was sich dahinter verbirgt und vielleicht den Wandel mitgestalten? Dann sollten Sie d-fine näher kennenlernen. Denn mit solchen Themen und vielen weiteren spannenden und anspruchsvollen Fragestellungen beschäftigen sich unsere Berater (m / w). Und sie beantworten die an sie gestellten Fragen durch die Kombination von Methoden und Modellen aus Ökonomie, Mathematik und Physik. Wissenschaft und Unternehmen, alles ist ständig in Bewegung.
Es gibt noch viel Platz für neue Denkansätze und unkonventionelle Ideen bei d-fine. Registrieren Sie sich auf unserer Homepage bis zum 2. Juli 2017. Je früher desto besser, denn die Teilnehmerzahl ist begrenzt. Wenn Sie also gerade dabei sind, Ihre akademische Karriere mit einem exzellenten Abschluss (MSc, Diplom oder Promotion) zu krönen und bereit sind, einen Schritt über die Grenzen zwischen Naturwissenschaft und Unternehmenspraxis zu gehen, dann sind wir gespannt auf Sie.
d-fine ist ein führendes europäisches Beratungsunternehmen mit Standorten in Frankfurt, München, London, Zürich und Wien. Mit über 600 hochqualifizierten Beratern unterstützen wir unsere Kunden – Banken, Versicherungen und Industrieunternehmen – bei anspruchsvollen quantitativen, prozessualen und technologischen Herausforderungen. Strategieberatung, Fachberatung, Technologieberatung: d-fine ist alles in einem.
d-fine. Die Spezialisten für Risk&Finance.
½-tägiger Workshop mit finanzmathematischen Vorträgen zum Themenkomplex Modellbewertung und Kontrahentenrisiko sowie Erfahrungsberichten aus unserer Consulting-Praxis.
Bewerbungsschluss ist der 2. Juli 2017.
Montag, 10. Juli 2017
Adina Apartment Hotel
Hamburg Michel
Neuer Steinweg 26
20459 Hamburg
d-fine GmbH
Svenja Dröll
An der Hauptwache 7
60313 Frankfurt am Main
T +49 69 907 37- 555
www.d-fine.com
Frankfurt, München, London, Zürich, Wien
Careers
MathFinance Openings
Senior Quant/ Consultant
We are looking for senior quant/ consultant in the areas of
Insurance
- Actuary with 5 to 7 years of experience in insurance or re-insurance
- Experience in quantitative Risk Management in relation to regulatory issues (Solvency II)
- Experience in Capital Management
Banking
- Quant with 5 to 7 years of experience in Banking, ideally in Trading
- Experience in quantitative Risk Management in relation to regulatory issues (Basel III)
- Experience in Capital Management
Investment
- Quant with 5 to 7 years of experience in Asset Management (Funds, Insurance and Family Offices), ideally with emphasis on Risk Management
- Experience in quantitative Risk Management in relation to regulatory issues (German KAGB and KARBV)
Please send us your CV to recruitments@mathfinance.com
Junior Quant
Do the following apply to you?
- Master degree or diploma in (business) mathematics or physics
- PhD or CFA is a bonus
- First experiences in mathematical finance is desirable
- Very good programming skills, e.g. C++, Python or Matlab
- Good language skills in German and English
- Outstanding analytical skills and a problem-solving attitude
- High motivation to develop your knowledge and skills
- Good communication skills and team spirit
Then we would like to hear from you. Please send us your CV to recruitments@mathfinance.com
