Editorial
Derivatives Risk Management and Aviation
Working in derivatives risk management and the cockpit of a plane has much in common. There are stunning similarities already in the number of screens and indicators one observes and needs to pay attention to while flying, and similarly while running a derivatives portfolio, see the panel in Figure 1. And the usual questions are: can I continue my position, or do I need to change something? Which adjustments do I make to fly smoothly? Do I need to abandon the flight?

Figure 1: Cockpit of a Single-Engine Mooney 20J
As in risk management, one needs to judge multiple factors at the same time: altitude (spot), airspeed (implied volatility), ground speed (historic/prevailing volatility), vertical speed indication (delta hedging in high gamma), wing level (skew), visibility (market data access), fuel consumption (margin in the account), weather (market turbulence), engine (risk management software), traffic rules (compliance), passenger safety (involvement of colleagues), traveling costs (sales and traders’ margin), paperwork (documentation, regulation), etc.
One of the main questions I am asked frequently is if one can have accidents in planes. While the answer is obvious, one tends to associate a (statistically) very small probability to aviation accidents. And in case of an accident, the probability of its occurrence assigned before becomes completely irrelevant.
| Ask yourself this question: Suppose you boarded an aircraft ready to fly to your destination and pilot announces that on the upcoming flight the probability of having an accident is twice as high as usual (but still 0.0002%). If you decide to take the flight, you get half the ticket cost refunded, but you have the option to leave the aircraft. Would you fly? |
I am trying to create awareness of probabilities of a hazard. Before we take off, let me illustrate how a treasurer assess financial risk.
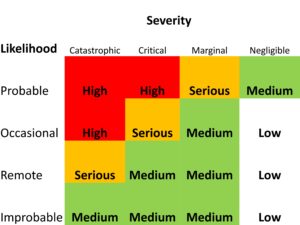
Figure 2: Aviation Risk Assessment Matrix
I have seen in many examples of risk management of floans (FX loans, loans in foreign currency) that the hazard of the exchange rate moving against the floan-taker is considered as only remotely likely to occur – and therefore the floan feels like a low risk decision. However, one often forgets to put it in relation to the severity of the outcome: A large move of the exchange rate can leave the corporate or city treasurer with a catastrophic loss that ruins the company or the municipality; the equivalent in aviation would be a fatal accident. In the risk assessment matrix, the likelihood of the hazard would be classified as remote (this classification depends on the assessor), and the severity of the outcome as catastrophic (this classification also depends on the assessor). The matrix shows that the risk is serious under this assessment.
There is a lot to learn from a risk assessment matrix I found in an aviation training program of the FAA (Federal Aviation Association): In this matrix (Figure 2) one considers the likelihood of a hazard occurring and the severity of its outcome. Applying the aviation risk assessment matrix is rather simple, but I consider it extremely useful also in a financial risk management context. Using it can prevent us to be penny wise pound foolish.
A lower interest rate in Swiss Franc (CHF) for decades has tempted many corporates and private people in the Euro zone (EUR/CHF), Poland (PLN/CHF) and Hungary (HUF/CHF) to become floanies (loan takers in foreign currency). A floan is a carry trade, no matter how you twist and turn it. Carry trades can fail, if the spot moves more and causes more loss than the interest the treasurer saves. For example, the Swiss France lost 30% of its value against Deutsche Mark in the seventies (Figure 3), and a short term history does often not reveal the potential spot movements ahead.
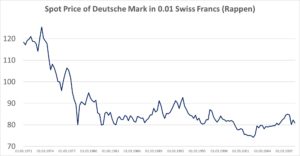
Figure 3: History DEM-CHF spot rates before 2007
The carry-traders forget to assess their risk and are then trying to blame the banks if the carry trade fails. While all the focus is given to the probability of the hazard, what is missing is a good assessment of its severity. If a floan creates a loss of 30% of the loan notional, and this is so much that the municipality would not be able to handle it, then the probability of its occurrence becomes irrelevant.
The next round of floans taken at a large scale with a serious risk is already on its way: in India, Brazil and in China, to name a few. Regular flying (as in Figure 4) can increase risk awareness and the aviation risk assessment matrix should very well become part of risk management. In case of an engine failure we want to land at the closest airfield. Can you spot it? Happy Landings!

Figure 4: La Llagonne Airfield in Sight?
—————————————————————————————————————————————————–
Upcoming Events
Online Webinar
In view of the uncertainty caused by the Coronavirus outbreak, MathFinance has decided to postpone its 20th annual MathFinance Finance conference to 1st and 2nd September to guarantee a safe and successful participation. The location remains unchanged. A majority of speakers have confirmed their attendance and the full agenda will be uploaded in due course.
For more information please visit:
https://mtf-old.ansichtssache.de/events/mathfinance-conference-2020/
————————————————————————————————————————————-
MathFinance Trainings
MathFinance is excited to host its new training offerings for 2020. For further details please click on the links below. Additionally, we also offer in-house training programmes on areas of interest covering Machine Learning, FX Options, Interest Rate Derivatives and Equity Derivatives.
Course: Machine Learning & Artificial Intelligence Applications for Financial Markets
Trainer: Dr. Thorsten Schimdt, Senior Financial Engineer, MathFinance & Professor for mathematical stochastics at University of Freiburg
Date: 16-18 September 2020
Format: Online training course, using Webex
Fees: EUR 2,500 p.p. EUR 2,000 p.p. if 2 or more people join from the same organization
More information: Machine Learning & Artificial Intelligence Applications for Financial Markets
Course: FX Options & Structured Products
Trainer: Dr. Uwe Wystup, Managing Director, MathFinance AG
Date: 13-14 July 2020, Singapore time-zone
Format: Online training course, using Webex
Fees: SGD 3,000 p.p. SGD 2,500 p.p. if 2 or more people join from the same organization
More information: FX Options & Structured Products
Course: Credit Risk Modelling: IFRS 9 & Stress Testing
Trainer: Dr. Bernd Engelman
Date: 13-14 August 2020
Format: Online training course, using Webex
Fees: EUR 1,500 p.p. EUR 1,200 p.p. if 2 or more people join from the same organization
More information: Credit Risk Modelling: IFRS 9 & Stress Testing
To enrol for any of the MathFinance training courses or for further inquiries, please mail us at: info@mathfinance.com
For further details on our other offerings please visit:
https://mtf-old.ansichtssache.de/trainings/
————————————————————————————————————————————-
————————————————————————————————————————————-
Digital Finance
Call for Papers
Special Issue on Artificial Intelligence, Machine Learning and Platform Innovation in Quantitative Finance (MathFinance Conference 2020)
Overview
Traditionally, Quantitative Finance has revolved around the development of parsimonious models that yield some economic understanding of financial markets. In recent years, there has been a change in this paradigm by embracing data-driven methods from AI and ML. Here are some reasons that explain this shift: greater amounts of financial data are available that require fast processing; financial analysis and computations are supplemented by non-financial data, such as textual data, in order to create new insights; data-driven methods allow to detect trends and market changes that would not be observed with a rigid model. At the same time, platform technology has taken over trading of spot and derivatives in financial markets. Pricing models, Greeks and risk calculation must be faster and more accurate than ever before. The special issue welcomes contributions that explore innovative uses of AI / ML methods and platform technology in Quantitative Finance. These can involve economic, quantitative, computational and technological aspects.
Speakers and participants of the MathFinance Conference 2020 are encouraged to submit their work, but the special issue also welcomes contributions from the community.
Editors of the Special Issue
Prof. Dr. Natalie Packham, Berlin School of Economics and Law
Prof. Dr. Uwe Wystup, Managing Director, MathFinance
Instructions for Submission
For submission, authors are requested to access the access the Editorial Manager at the following URL: http://www.editorialmanager.com/dfin/default.aspx. Please answer “Yes” when asked if your manuscript belongs to a special issue and select the special issue in the list that will pop up.
Potential authors are reminded that all papers that are finally accepted for this special issue will be subject to format restrictions complying with the publisher’s standards. To speed up publication, and to ensure a unified layout throughout the special issue, authors are kindly advised to use LaTeX. Springer’s LaTeX template (click here) can be used to prepare source files (please choose the formatting option “smallextended”). The authors are highly recommended not to modify the class file by introducing personal settings and/or definitions.
Important Dates
Deadline for paper submission: 30 June
First-round decisions: 31 July
Deadline for second-round submission: 15 September
Final decisions: 31 October
About Digital Finance
The journal is a top tier peer-reviewed academic and practitioner journal that publishes high-quality articles with a focus on digital finance and innovation as well as on the analysis of digital and internet innovations on financial services and the economy. The journal publishes theoretical or empirical, qualitative or quantitative papers of interest to academics, practitioners, and regulators with the emphasis on empirical, financial market, and investment innovation, financial policy research and recommendations related to improving the welfare in the digital economy. Further details on this journal are available on the Springer website: https://www.springer.com/42521
